A New Musical Scale
Sun 30 October 2016
Introduction
Pythagoras, in the 6th century BCE, made the observation that musical intervals were perceived as consonant when the ratio of component frequencies could be expressed as ratio of simple, whole numbers. The simplest ratio, of course, is \(2\), which represents the octave (notes an octave apart vary in frequency by a factor of two). The next simplest ratio is \(\frac{3}{2}\), which represents a perfect fifth. In Pythagorean tuning that perfect fifth becomes the generator interval, with scale degrees calculated by walking a circle of \(\frac{3}{2}\) fifths.
More recently, researchers have found that even infants respond in a way that suggests they too find such ratios more consonant or pleasant. Research also suggests that a capella groups tend to gravitate towards such intervals (the voice not being a fixed-tuning instrument).
For many years Western tuning systems worked with these ratios (and some musical traditions, such as Indian traditional music, still use forms of Just Intonation), but eventually different approaches were pursued. A perceived weakness of just intonation is that while many intervals sound consonant, there are some which are distinctly dissonant. Thus, for any instrument with a fixed tuning, certain scales and/or keys will display some very dissonant intervals, sounding more like out-of-tune notes than defined and intentional intervals.
One of the first approaches employed to address this was meantone tuning, in which the generator interval is tweaked slightly (usually narrowed by a small amount), so that while the consonant intervals end up ever so slightly out of tune (in terms of simple ratios), the traditionally dissonant intervals are made more consonant. With this approach it becomes easier to play in a wider variety of keys on a fixed-tuning instrument.
Another approach is even temperament, in which the intervals between any two contiguous notes is the same. While some mention of this concept can be found as early as the 4th century BCE, it wasn't until the Renaissance (around the 16th century) that this became a common approach in Western music. But once that program was undertaken it continued to gather strength, so that today it is used almost exclusively in all forms of Western music, from pop to art.
This is not an unreasonable approach, and it represents a kind of culmination in the attempt to compromise between dissonant and consonant intervals. It allows any fixed-tuning instrument to play any key equally. But if one examines the ratios of the current system, where each adjacent interval is \(\sqrt[\frac{1}{12}]{2}\), the twelve degrees of the chromatic scale look like:
where each degree is shown as a ratio above the first tone.
Furthermore, because of the equality of the intervals, we can calculate all intervals that occur between any two notes. This is the same set (with the unison and octave omitted):
All intervals, with the exception of the octave, are slightly out of tune (in other words, only one interval can be expressed as a simple ratio). So while one could argue that each key signature sound equally good, one could also argue that they sound equally bad.
Within the domain of electronically generated/computer generated music, the constraint of fixed tuning doesn't carry the weight that it once did. Every composition can have its own tuning (or tuning system), chosen for the specifics of the composition itself. This can alleviate the issue with dissonant intervals, because a tuning can be chosen for any composition to minimize their occurrence. Because I work in these domains, I undertook an exploration of novel tuning systems. This essay describes the approach and a scale/tuning which I have found to be interesting.
Why Simple Ratios?
It's probably impossible to give a definitive answer as to why we find simple ratios consonant, but we can speculate. There any many possible avenues of exploration; what I'd like to focus on here is in the physics of sound production.
Tuned Sounds
A sound with a perceivable frequency (pitch) is a periodic function. The shape of that waveform (and its change in time) is what gives a sound its unique character. It's how we recognize different voices and different instruments.
In the 19th century, while working on the problem of heat flow, Jean-Baptiste Joseph Fourier noticed that any periodic function (such as, in our case, a tuned note) can be represented by a series (perhaps infinite) of simpler periodic functions, such as a sine or cosine. This is a useful insight in our analysis of why sound sounds the way that it does.
This utility is perhaps easiest to explain if we examine a specific example, and for this I'll chose a vibrating string (but the situation is the same for many sound generators, such as a struck bar or the resonating column of air that you will find in many instruments).
When a physical impulse is imparted to a fixed string (by plucking, bowing, etc.) is begins vibrating at a frequency that is determined by the string's length and diameter, as well as it's tension:
If that were the end of it all strings would sound more-or-less the same, because they would all have the same waveform. But that isn't the end of it. Other vibratory modes will also be excited, and given that the ends of the string are fixed (and they modes arise at the same tension and string diameter), these vibratory modes will be at a integral multiple of this fundamental tone. So, for example, the first four harmonics would look something like:
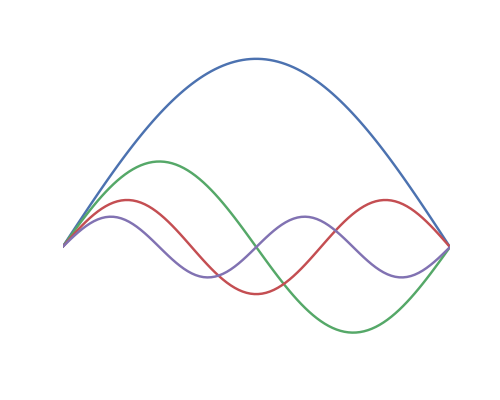
If the fundamental (the blue line) were 100 Hz, the second harmonic (the green line) would be at 200 Hz, the third at 300 Hz, and the 4th at 400 Hz. Thus the harmonics themselves exist in simple, whole-number ratios. Through Fourier analysis any waveform can be analyzed, and it is found that the timbre of the sound relates to the relative strength (and to extent phase) of these harmonics.
Every tuned sound that we hear is a superimposition of tones which are related to each other by simple ratios. This is true from a mathematical perspective, and there is also evidence that our ears and brains actually work in this way from a physiological perspective. Our ears, for example, seem to perform something of a spectral analysis, as different parts are sensitive to different frequencies.
Given the fact that all pitched sounds that we hear already encode simple ratios of tones, perhaps it isn't too surprising that this colors our perception or multiple tones (harmony). It is possible that we have evolved to apprehend these ratios, because in a basic way this is a fundamental property of sound.
Scale Generation
As mentioned above, equal temperament (also called Equal Division of the Octave) has assumed a dominant position in Western music composition (the exception being composers who explicitly set out to explore alternate and/or non-Western tunings). However, this hasn't prevented musicologist and theorists from examining alternative techniques, and they have done so with gusto. Many alternatives have been suggested and explored. The work documented here focuses on one such alternative, the harmonic scale.
The Harmonic Scale
Extending the discussion of the harmonic nature of sound, it is possible to use the harmonic series to generate the notes of a scale. If, for example, we take the first 10 harmonics of a tone, we end up with the following series:
Remember, though, that an octave is a factor of two, and we perceive notes separated by octaves as somehow the same note. Therefore it is common in musicology to normalize such an interval, taking each note and either multiplying of dividing by a power of two to make the note fall within a single octave (or, numerically, making it fall between the value of 1 and 2). In doing this the above series would be transformed to the following:
The \(\frac{9}{8}\) interval, for example, comes from the penultimate note, 9, when scaled to the octave:
(in other words, its the ratio 9 scaled down by three octaves).
It is also possible -- and common -- to reference the ratios to a harmonic different than the fundamental. So, for example, if we were interested in referencing things to the third harmonic instead of the first, our original series would be:
Dividing each interval by three and then normalizing to the octave yields:
For the scale documented here I took a long harmonic series -- 30 harmonics, referenced to the fourth harmonic. I used a long series so there would be many potential notes from which to choose the scale (the method of selection will be described below). This scale has 16 degrees (including the unison and octave):
The issue with the series is that, while it is harmonically complex, it is harmonically very complex. If we examine all the distinct intervals within an octave (in the same way that we did for the even tempered scale above): we end up with a large set of distinct intervals:
That is a lot of harmonic complexity!
The way of handling the complexity it to choose a subset of notes from this scale in he same way that the standard major and minor scales are a chosen subset of the 12 chromatic tones of the standard tuning. But to do this we have to have a way of estimating which intervals may be consonant or dissonant.
Consonance and Dissonance
In order to characterize the feel of a scale or mode, it is useful to define a metric that measures an interval's consonance. And while musicologist have done formal work in this, I decided to create some simple metrics that proxy for the fact that "the ratio of simple whole numbers sounds consonant." Much more complicated (and better defined) metrics are possible, but I wanted to use a simple metric as a proof of concept.
The metric I chose for this scale is to take all of the distinct intervals within the scale and to sum up the numerators and denominators of all intervals. The lower the number the smaller the composite numbers for the intervals, and the more consonant the scale is rated.
It is also useful to visualize the consonance of a given scale. For this we can create a heat map that compares every degree to every other degree. For the harmonic scale given above, this follows:
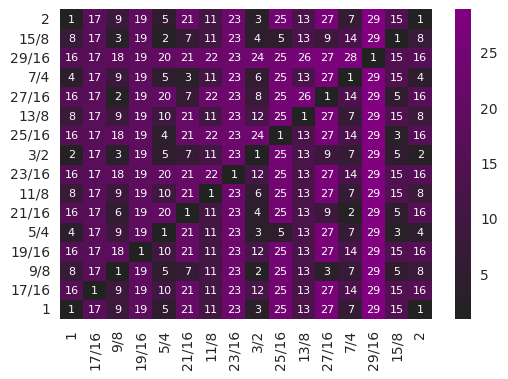
Each matrix position is the interval between two degrees, the diagonal being each note played against itself. The label is the denominator of the interval as expressed in lowest terms (the thought being that lower numbers are more consonant).
To create the mode I chose seven tones (eight including the octave) from the scale and calculated the consonance matrix. As it turns out there are 3003 different ways to choose those tones from the full scale, and to evaluate each scale requires the evaluation of 64 separate intervals. Overall 192,192 intervals had to be created and calculated to find the scale that minimized the metric function. This is a lot of computation, but is fairly trivial for modern computing technology (the combinatorial analysis takes less than a minute on a reasonably powered modern computer).
The Scale
To recapitulate, the following parameters were used:
- First harmonic: 4
- Last harmonic: 30
- Number of tones: 7 (8 if octave is included)
- Metric: Minimize the sum of the numerators and denominators of all distinct intervals within the mode.
The scale that minimizes the metric for the given parameters is as follows:
And its consonance matrix is given by:
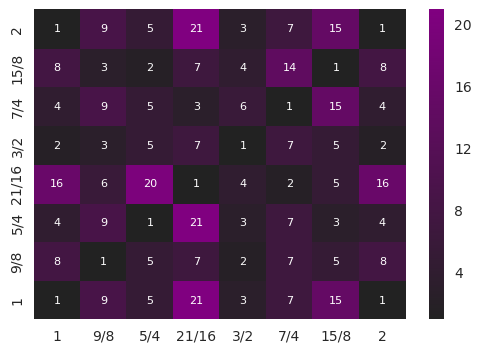
I am not a musicologist -- this is just an interest of mine -- but in my (admittedly) cursory reading of the literature I could find no reference to this particular scale. It is possible that it has been used before (but if so I don't think it has been widely used). It is also possible that it is a new scale which has not yet been explored.
The Simplest Expression
The above parameters describe how I originally came across the scale, but they don't represent the simplest formulation. The scale is also found in the harmonic scale constructed from the 1st to 21st harmonic:
- First harmonic: 1
- Last harmonic: 21
which yields, when normalized:
When the same metric is applied, the scale results:
Harmonic Complexity
If you recall, the standard 12 tone Equal Division of the Octave has a small set of distinct intervals:
If we examine the intervals in this scale, it is a slightly larger set:
Some of these intervals are consonant, whereas some (for example \(\frac{21}{20}\)) will sound somewhat dissonant.
What Does it Sound Like?
The following widget plays two clips: a small riff in the standard major scale in 12-EDO, and the same riff played in the scale described above:
At first the scale sounds a little foreign, but in working with it I've found that the ear quickly adapts and the scale subsequently starts to make musical sense.
It is also interesting to compare this scale numerically to a commonly used scale, such as the 12-EDO major scale. In the following table this is done, with the first note of the two scales pegged to A = 220 Hz:
| Major Freq | Harmonic Freq | Delta(Cents) |
|---|---|---|
| 220.0000 | 220.0000 | 0.0000 |
| 246.9417 | 247.5000 | -3.9100 |
| 277.1826 | 275.0000 | 13.6863 |
| 293.6648 | 288.7500 | 29.2191 |
| 329.6276 | 330.0000 | -1.9550 |
| 369.9944 | 385.0000 | -68.8259 |
| 415.3047 | 412.5000 | 11.7313 |
| 440.0000 | 440.0000 | 0.0000 |
We can also examine the scale's relationship to the (harmonic) minor. This is even further removed:
| Minor Freq | Harmonic Freq | Delta(cents) |
|---|---|---|
| 220.0000 | 220.0000 | 0.0000 |
| 246.9417 | 247.5000 | -3.9100 |
| 261.6256 | 275.0000 | -86.3137 |
| 293.6648 | 288.7500 | 29.2191 |
| 329.6276 | 330.0000 | -1.9550 |
| 349.2282 | 385.0000 | -168.8259 |
| 415.3047 | 412.5000 | 11.7313 |
| 440.0000 | 440.0000 | 0.0000 |
(A cent is an equal division of the octave too, with 1200 comprising a single octave.)
In the comparison to the major scale, the largest delta is about 69 cents, which is the better part of a semitone (which is defined as 100 cents in 12-EDO).
Compositions
Update: The album is out! You can hear seven, quality-crafted bespoke compositions with this scale at the above link.
Also, below is a short work (a sound-scape) using this scale:
If you like the piece you can download it by right clicking on this, but keep in mind this is a work in progress and may change.
Further Work
This work was undertaken with software I wrote specifically for the exploration of novel tunings. It contains additional scale generators (meantone, syntonic, EDO, etc.) and metrics. Given the parameterizations and options available, if should be possible to identify many potentially interesting scales for exploration.
I have released this software as an open-source project, and it's probably mature enough to be used by those with a little knowledge of Python and musical scales. See this post for details.