Printing Three Dimensional Fractals

Thu 18 August 2016

A few years ago people started exploring three dimensional fractals, which are extensions to the standard 2-dimensional Madelbrot set. One of the first was discovered by Daniel White and named the mandelbulb. Most (if not all) of these three dimensional structures are generated by extending and generalizing the concept of complex exponentiation into multiple dimensions.

The standard Mandelbrot set is defined by:

\begin{align*} z_{n+1} &= {z_n}^2 + c \\ z_0 &= 0 + 0i \end{align*}

where c is a point taken from the complex plane, \(x+iy\). The equation is iterated a certain number of times, and set membership is determined by the status of z: if it remains bounded then the point c is in the set, otherwise it is outside. There are several practicalities -- how many times to iterate, the threshold to determining unboundedness, etc. -- but that's it in a nutshell. Because there are two components to a complex number, this is a two dimensional figure. How can it be extended to higher dimensions?

As you may remember from math class, exponentiation in the complex plane, i.e.

\begin{equation*} z^n \end{equation*}

can be given a geometrical interpretation. If we represent z in polar coordinates (r, theta) in a plane where x is given by the real component of z and y is given by the imaginary component, then raising a number to a power n is equivalent to raising the r component to n and multiplying theta by n.

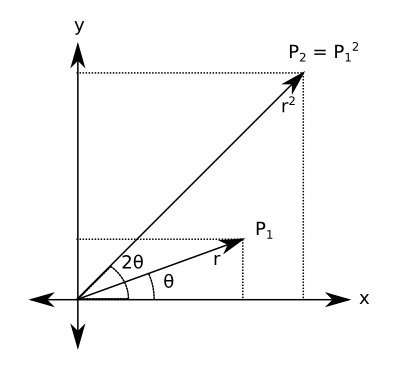
With the mandelbulb the concept of exponentiation is extended to three dimensions with the following equation:

\begin{equation*} \left(x,y,z \right)^n = r^n \cdot \left(sin(\theta \cdot n) cos(\phi \cdot n), sin(\theta \cdot n) sin(\phi \cdot n), cos(\theta \cdot n)\right) \end{equation*}

where:

\begin{align*} r &= \sqrt{(x^2 + y^2 + z^2)} \\ \theta &= tan^{-1}\left({\frac{\sqrt{x^2+y^2}}{z}}\right) \\ \phi &= tan^{-1}\left(\frac{y}{x}\right) \end{align*}

(which is to say r, theta, and phi are the standard spherical coordinates). This is analogous in a straight-forward way to the two-dimensional case, with r increased in the same way as the 2-D case and the polar coordinates multiplied by n in the same way that theta is in the 2-D case. This, I believe, is an idiosyncratic (and unique) definition, but one can see the motivation behind it in this analogy. (I have also done some investigations with other idiosyncratic definitions, which are documented elsewhere).

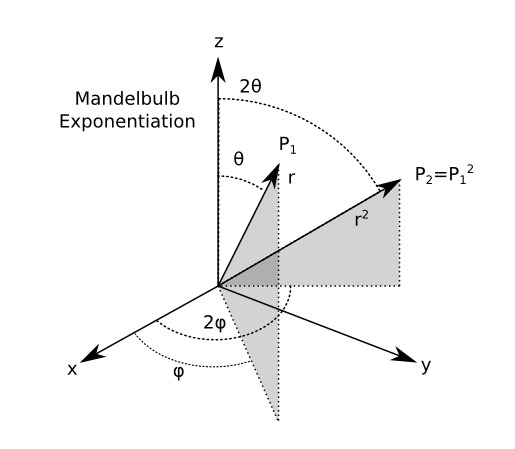
Given the above definition, a mandelbulb of degree N is defined by

\begin{equation*} z_{n+1} = {z_n}^N + c \end{equation*}

where c is now the triplet {x,y,z}.

Different orders of mandelbulb produce different results, and a sweet-spot exists between, say, 4 and 10. Many of the pictures posted on-line are of order eight, as is the following render (which was created by a ray-tracer I wrote in Haskell).

(Click to Enlarge)

The problem is that you see many beautiful images of these structures, but they are all flat projections.

Printing a Fractal

Because these are three dimensional objects, it is possible (and interesting) to actually instantiate them in three dimensions. With the advent of 3-D printing this has become pretty easy.

I couldn't find any software that was capable of producing the 3-D models, so I wrote my own package (again in Haskell). It makes use of the marching tetrahedra algorithm, which is an algorithm that can be used to render implicit surfaces in volumetric fields. The software produces an STL file (which is commonly used in stereo lithography) that can be in turn imported into a program like meshlab for clean-up, vertex reduction, etc. STL is a format widely understood in the 3-D printing space.

Below is the surface model of the eighth-order mandelbuld shown above:

Click For Other Views and Enlargement

I originally did this work a few years ago (2011) and 3-D printers will still something of a novelty, so I had to submit the models to a service bureau (Shapeways). At the time printing was quite expensive -- being charged by the cubic centimeter -- so I had to print the models small. The company also imposed restrictions on the number of facets that a model could contain, so the resoltions was somewhat limited. As far as I could tell from searching on-line no one had done this, but as I said this work was done a while ago, so it's possible that printing these structures has become common.

The Finished Products

I printed two mandelbulbs: the eighth-order shown above, and a fourth-oder model, shown below:

Click for other views

As mentioned above these were printed small, so I appologize for the quality of the photographs. For scale, the figures are about 3cm across.

Click for other views