Introduction

The "flower of life" is a modern term referencing a very old geometric pattern. According to the Wikipedia Article the figures have been found at, for example, the Temple of Osiris (6th century BCE) and Herod's Palace (1st century BCE).

At it's simplest, it can be formed by overlapping circles along some rotational symmetry group. One of the most common is an arrangement of seven circles:

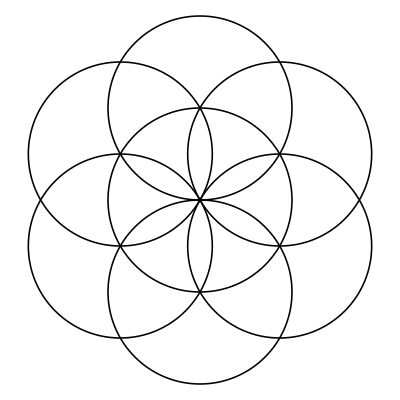
Another common arrangement is on a square grid:

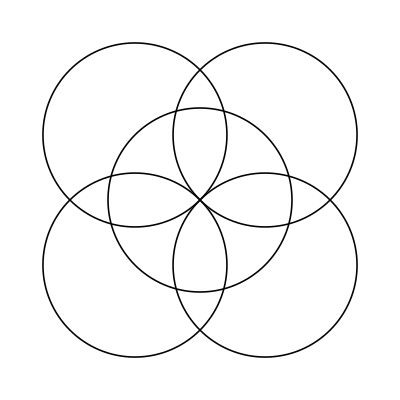
Translations

The above illustrations show what could be called a single floret. Commonly these patterns are repeated in translation, forming a larger tessellation of the plane. As an example, a page from Leonardo da Vinci's notebook shows an example of the repeated pattern:

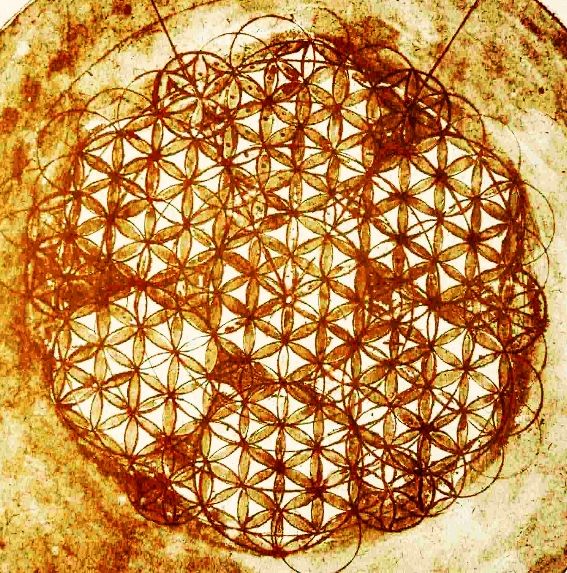
This tessellation is cosmopolitan, and can be found in many historical sites.

In this essay, however, I'll be examining extending the figure through recursion.

Iterating on the Flower

Instead of translating and repeating, we can also extend the pattern in depth.

So, for example, we can take a circle:

The replace with a three-fold flower, once:

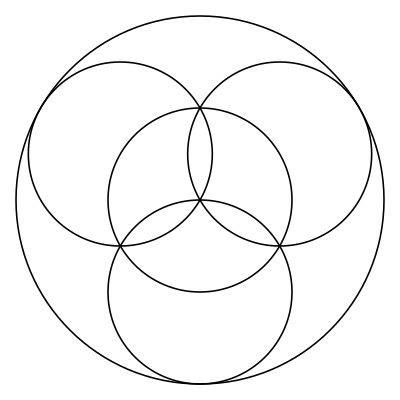
Then, in each of the inner circles we can place an identical figure:

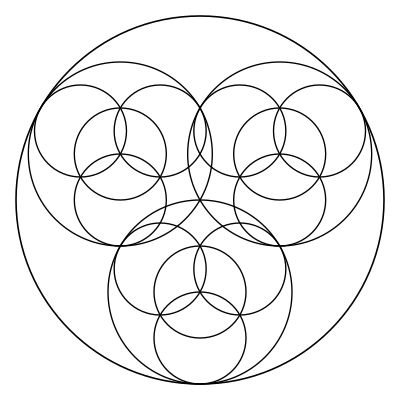
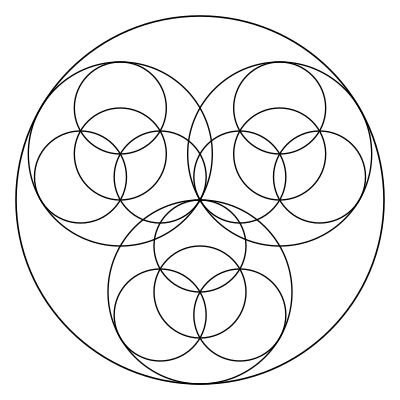
That represents the basic process of recursion, but there are a few variations that can be employed for different aesthetics. For example, in the above we placed the self-similar figures at the same rotation, but we could rotate them \(\pi\) such as in:

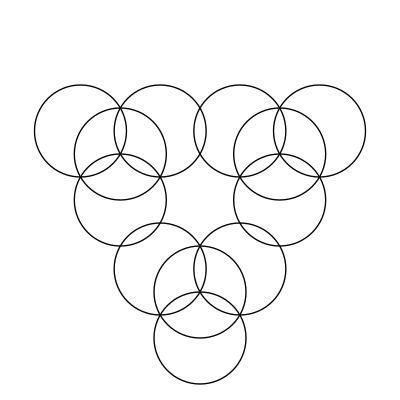
We could also just draw the circles at the lowest level, such as in:

With these things in mind, we can examine some recursion figure for a few different symmetries that produce attractive figures.

Three-Fold Symmetry

One interesting figure can be produced by recursing the three-fold symmetric flower down several levels. For example, if we take it down four levels, we start to see something of a familiar pattern arise:

Click For Zoom

The pattern becomes even more apparent it we take it down eight levels:

Click For Zoom

One would need to be seriously lacking in imagination to not see the Sierpinski triangle in this figure. This can be seen even more clearly if we look at a detail of a figure recursed 10 levels:

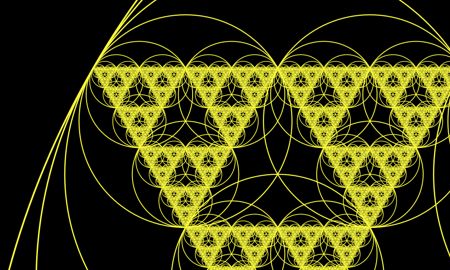
Click For Zoom

Five-fold Symmetry

One of my personal favorites is produced by taking a five-fold flower and recursing it deeply, reorienting each level by a rotation of \(\pi\). For example, a recursion of six levels:

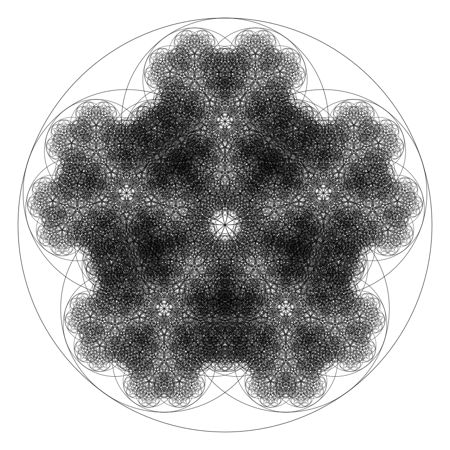
Click For Zoom

This figure also produces an attractive variant when only the inner circles are drawn. For example, taking the figure down seven levels:

Click For Zoom

If we don't rotate by \(\pi\) in our successive iterations, the figure produced looks different, but it still somewhat striking. This figure is for a recursion depth of 9:

Click For Zoom

Seven-Fold

Lastly: since three and five both produce interesting results, will seven? The next illustration shows that it does, in a figure four levels deep and only drawing the innermost circles:

Click For Zoom

The full version (with all circles drawn, not just the inner-most) also produces an attractive figure:

Click For Zoom

Conclusions

No conclusions -- just some pretty figures!